100番です。
袋から連続で2個のボールを取り出したときに、同じ色のボールが出る確率をちょうど2分の1にするには、何個のポールを入れたらいいでしょうか。という問題です。
初めに思いついた方法は時間がかかりすぎてだめでした。
式を立てていろいろいじっていたら解けました。
青のボールの数をb、全体のボールの数をaとすると、1つめに青の出る確率は、b/a、その後で2つめも青になる確率は(b-1)/(a-1)です。問題は、これを掛けたものが1/2になる場合ということです。
ということで作ったのが、最初のコードです。ところが、実行してみると1時間たっても1桁も進みません。5時間ほどぶんまわしてみたのですが、答えが出ません。だいたい、平方根の逆数を使っているので、そんなに桁数が大きいとなると精度に入らない可能性があります。この方法はあきらめました。
ちなみに、小さな数であれば、ちゃんと答えがでます。桁を増やしながら計算してみると、
最後のところくらいで1分を超えてしまいます。
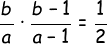
のようになります。あれこれいじくりまわしたところ(最初ひどいミスをしていて、1時間くらいハマりました。)、ペル方程式の形に持っていくことができました。
&=a(a-1)\\[+5pt] 2(b^2-b)-(a^2-a)&=0\\[+5pt] 2(b^2-b+\frac{1}{4}-\frac{1}{4})-(a^2-a+\frac{1}{4}-\frac{1}{4})&=0\\[+5pt] 2(b^2-b+\frac{1}{4})-\frac{1}{2}-(a^2-a+\frac{1}{4})+\frac{1}{4}&=0\\[+5pt] 2(b-\frac{1}{2})^2-\frac{1}{2}-(a-\frac{1}{2})^2+\frac{1}{4}&=0\\[+5pt] \frac{2}{4}(2b-1)^2-\frac{1}{2}-\frac{1}{4}(2a-1)^2+\frac{1}{4}&=0\\[+5pt] 2(2b-1)^2-2-(2a-1)^2+1&=0\\[+5pt] (2a-1)^2-2(2b-1)^2&=-1 \end{align*} "\fn_cs \begin{align*} \frac{b}{a} \cdot \frac{b-1}{a-1}&=\frac{1}{2}\\[+5pt] 2b(b-1)&=a(a-1)\\[+5pt] 2(b^2-b)-(a^2-a)&=0\\[+5pt] 2(b^2-b+\frac{1}{4}-\frac{1}{4})-(a^2-a+\frac{1}{4}-\frac{1}{4})&=0\\[+5pt] 2(b^2-b+\frac{1}{4})-\frac{1}{2}-(a^2-a+\frac{1}{4})+\frac{1}{4}&=0\\[+5pt] 2(b-\frac{1}{2})^2-\frac{1}{2}-(a-\frac{1}{2})^2+\frac{1}{4}&=0\\[+5pt] \frac{2}{4}(2b-1)^2-\frac{1}{2}-\frac{1}{4}(2a-1)^2+\frac{1}{4}&=0\\[+5pt] 2(2b-1)^2-2-(2a-1)^2+1&=0\\[+5pt] (2a-1)^2-2(2b-1)^2&=-1 \end{align*}")
この最後がペル方程式の形です。
ペル方程式は前にも出てきました。あとは最小解さえわかれば、答えがでそうです。
最小解はなんだろうと調べる間もなく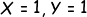
が思い付きました。
あとは漸化式に初期値を突っこんで、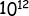
を超える最初の値を出すだけです。
答えはX,Yからa,bを出す式を作って計算です。
上が正解で、下が遅いやつです。
袋から連続で2個のボールを取り出したときに、同じ色のボールが出る確率をちょうど2分の1にするには、何個のポールを入れたらいいでしょうか。という問題です。
初めに思いついた方法は時間がかかりすぎてだめでした。
式を立てていろいろいじっていたら解けました。
青のボールの数をb、全体のボールの数をaとすると、1つめに青の出る確率は、b/a、その後で2つめも青になる確率は(b-1)/(a-1)です。問題は、これを掛けたものが1/2になる場合ということです。
方法その1
1回目と2回目の確率は、aやbが大きくなるとほとんど同じになり、それぞれ√2に近い値になります。1回目の確率の方が大きいので、あるaに対してbは、「b/aが√2よりちょっと大きくなる」ように決めてやることができます。ということで作ったのが、最初のコードです。ところが、実行してみると1時間たっても1桁も進みません。5時間ほどぶんまわしてみたのですが、答えが出ません。だいたい、平方根の逆数を使っているので、そんなに桁数が大きいとなると精度に入らない可能性があります。この方法はあきらめました。
ちなみに、小さな数であれば、ちゃんと答えがでます。桁を増やしながら計算してみると、
user> (time (pe100 10N))
"Elapsed time: 0.237575 msecs"
[15N 21N]
user> (time (pe100 50N))
"Elapsed time: 2.299302 msecs"
[85N 120N]
user> (time (pe100 200N))
"Elapsed time: 15.118969 msecs"
[493N 697N]
user> (time (pe100 100000000N))
"Elapsed time: 79792.608028 msecs"
[112529341N 159140520N]
最後のところくらいで1分を超えてしまいます。
方法その2
題意を数式にすると、のようになります。あれこれいじくりまわしたところ(最初ひどいミスをしていて、1時間くらいハマりました。)、ペル方程式の形に持っていくことができました。
この最後がペル方程式の形です。
ペル方程式は前にも出てきました。あとは最小解さえわかれば、答えがでそうです。
最小解はなんだろうと調べる間もなく
あとは漸化式に初期値を突っこんで、
答えはX,Yからa,bを出す式を作って計算です。
上が正解で、下が遅いやつです。
0 コメント:
コメントを投稿