辺の長さと面積が整数になる、「ほぼ正三角形」を見つける問題です。
始めに総当たりで解くやつを作ったら、10時間かかりました。さすがにこれはだめなので、恒例の逆から考えるパターンです。
問題の三角形で、等しい辺の長さをa、残りの辺の長さを2b、高さをhとすると、a,b,hがピタゴラス数になるので、それぞれの辺は、
・パターンA
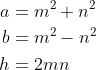
もしくは、
・パターンB
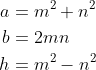
と表わすことができます。問題の条件から、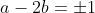
です。 パターンAの場合、
-2(m^2-n^2)=\pm 1\\ m^2-3n^2=\pm 1 \end{align*} "\begin{align*} a-2b=\pm 1\\ (m^2+n^2)-2(m^2-n^2)=\pm 1\\ m^2-3n^2=\pm 1 \end{align*}")
となります。これって、前にやったペルの方程式の形です。この形になったら、最小の1つがわかれば残りは計算でもとめられます。
さて、パターンBの方はどうかというと、
-2\cdot 2mn=\pm 1\\ m^2-4mn+n^2=\pm 1\\ m^2-4mn+4n^2-4n^2+n^2=\pm 1\\ (m-2n)^2-3n^2=\pm 1 \end{align*} "\begin{align*} a-2b=\pm 1\\ (m^2+n^2)-2\cdot 2mn=\pm 1\\ m^2-4mn+n^2=\pm 1\\ m^2-4mn+4n^2-4n^2+n^2=\pm 1\\ (m-2n)^2-3n^2=\pm 1 \end{align*}")
こんな風に、同じ形に持っていくことができます。
後は、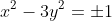
形のペルの方程式の最小解がわかればいいのですが、問題に、a=5、b=3という値が出ているので、これから求めると、(2,1)であることがわかります。
周の長さをx,yで表わすと、パターンAの場合は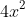
、パターンBの場合は、^2 \end{align*} "\begin{align*} 2(x+3y)^2 \end{align*}")
となります。
これで解いたのが2つめです。
なんと、1msec以下の時間で解けます。
すごい。
始めに総当たりで解くやつを作ったら、10時間かかりました。さすがにこれはだめなので、恒例の逆から考えるパターンです。
問題の三角形で、等しい辺の長さをa、残りの辺の長さを2b、高さをhとすると、a,b,hがピタゴラス数になるので、それぞれの辺は、
・パターンA
もしくは、
・パターンB
と表わすことができます。問題の条件から、
となります。これって、前にやったペルの方程式の形です。この形になったら、最小の1つがわかれば残りは計算でもとめられます。
さて、パターンBの方はどうかというと、
こんな風に、同じ形に持っていくことができます。
後は、
周の長さをx,yで表わすと、パターンAの場合は
これで解いたのが2つめです。
なんと、1msec以下の時間で解けます。
すごい。
0 コメント:
コメントを投稿