これもファレイ数列の問題です。
なんか、もうちょっといい方法が見つかりそうだんだけれども断念。
まあ、1分弱で解けたからいいということにしよう。
ファレイ数列の個数は、
※wikipediaの画像を勝手に拝借してみた。
と表わせるとのとのこと。 ここにでてくるφ(m)は前に出てきた、オイラーのトーシェント関数。
このまま計算すると、1から1000000までの数を全部素因数分解する必要があって、ちょっと大変なんで、最初は20分近くかかってしまった。
でも、素因数分解の関数(factors)を前のやつからちょっと工夫してやったら、1分を切った。
factorsはもうちょっと高速化できるかもしれない。
百万までの素数を作るのに、5秒くらいかるので、それを入れたら1分を切れないねぇ。
- phi-n
φ(n)を求める関数。
このとおり。
こういうふうに書けるところがClojure(lisp)が好きな理由だね。
- pe-72
ファレイ数列の式の通りの計算。
でも、公式の場合、0と1を含んだ個数で、PEの問題は両端を含まないので、
公式の結果から2を引いたものが答え。 ここちょっとはまった。
なんか、もうちょっといい方法が見つかりそうだんだけれども断念。
まあ、1分弱で解けたからいいということにしよう。
ファレイ数列の個数は、
※wikipediaの画像を勝手に拝借してみた。
と表わせるとのとのこと。 ここにでてくるφ(m)は前に出てきた、オイラーのトーシェント関数。
このまま計算すると、1から1000000までの数を全部素因数分解する必要があって、ちょっと大変なんで、最初は20分近くかかってしまった。
でも、素因数分解の関数(factors)を前のやつからちょっと工夫してやったら、1分を切った。
factorsはもうちょっと高速化できるかもしれない。
百万までの素数を作るのに、5秒くらいかるので、それを入れたら1分を切れないねぇ。
- phi-n
φ(n)を求める関数。
このとおり。
こういうふうに書けるところがClojure(lisp)が好きな理由だね。
- pe-72
ファレイ数列の式の通りの計算。
でも、公式の場合、0と1を含んだ個数で、PEの問題は両端を含まないので、
公式の結果から2を引いたものが答え。 ここちょっとはまった。
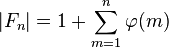


0 コメント:
コメントを投稿